Applying Lossless Compression and k-Nearest Neighbors for Text Classification
In the past weeks, an intriguing article was published on text classification. This article aims to provide simple but effective text classification using k-nearest-neighbors (kNN) and gzip, in contrast to Deep Neural Networks (DNNs). Although DNNs yield high results in text classification, they require extensive processing, millions of parameters, and a large number of labeled data. However, this article suggests a lightweight method that delivers good results without requiring any parameters or training. In this post, we will test this application using a dataset consisting of approximately 300 Turkish questions and answers related to law.
Related Studies and Approach
The article also mentions previous studies in this field, which were conducted using minimum cross entropy but did not produce efficient results. The explanations, formulas, and diagrams in this section are taken directly from the article.
Text classification with compressors can be divided into two main approaches:
Using Shannon Information Theory for entropy estimation and approximating Kolmogorov complexity and using information distance. The approach primarily uses a text compression technique called Prediction by Partial Matching (PPM) and applies it for topic classification. This approach estimates the cross-entropy between the probability distribution created with a given document d for a specific class c: Hc(d).
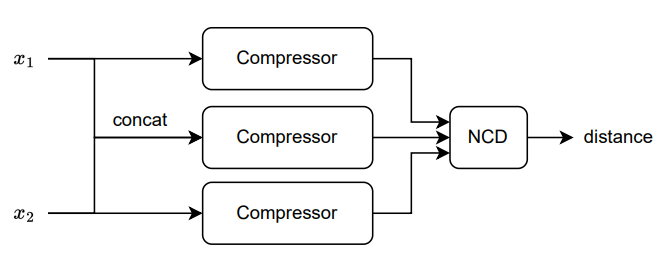
The article’s approach to this topic consists of a lossless compressor, a compressor-based distance metric, and a k-nearest neighbor classifier. Lossless compressors try to represent information using fewer bits, assigning shorter codes to symbols with higher probability.
For example, x1 belongs to the same category as x2, but belongs to a different category than x3. Assuming C(·) represents the compressed length, we will find C(x1x2) — C(x1) < C(x1x3) — C(x1); here, C(x1x2) denotes the compressed length of the combination of x1 and x2.
To measure the shared information content between two objects, Bennett et al. (1998) define the information distance E(x,y) as follows:
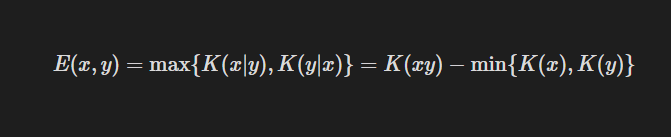
E(x,y) equates the similarity with the shortest program length needed to transform one object into the other.
The uncomputability of Kolmogorov complexity hinders the computability of E(x,y), hence Li et al. (2004) propose the Normalized Compression Distance (NCD), using the compressed length C(x) of real-world compressors to approximate Kolmogorov complexity K(x). The formula is as follows:
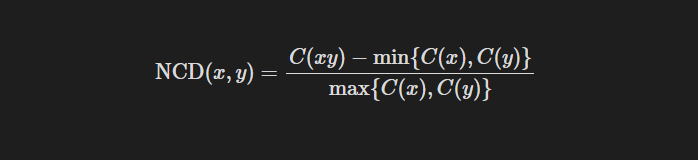
Here, C(x) represents the length after x has been compressed at the highest rate by the compressor. Generally, the higher the compression rate, the closer C(x) is to K(x).
We can use the kNN with the distance matrix provided by the NCD for classification. Our method can be implemented with 12 lines of Python code:
for (x1, _) in test_set:
Cx1 = len(gzip.compress(x1.encode()))
distance_from_x1 = []
for (x2, _) in train_set:
Cx2 = len(gzip.compress(x2.encode()))
x1x2 = " ".join([x1, x2])
Cx1x2 = len(gzip.compress(x1x2.encode()))
ncd = (Cx1x2 - min(Cx1, Cx2)) / max(Cx1, Cx2)
distance_from_x1.append(ncd)
sorted_idx = np.argsort(np.array(distance_from_x1))
top_k_class = [train_set[idx][1] for idx in sorted_idx[:k]]
predict_class = max(set(top_k_class), key=top_k_class.count)
Data Preparation and Testing the Approach
This part of the post is a bit experimental, and I believe, rather amateurish. Firstly, I downloaded my ChatGPT data and then split them into questions and answers. I assigned my data as questions, and the responses from GPT as answers, and converted them into a csv file. I then split it into train and test sets, but my approach here was as if I was training a DNN. I then conducted a test, and the results were somewhat successful.
import gzip
import numpy as np
import csv
dataset = []
with open('dataset.csv', 'r', newline='', encoding='utf-8') as file:
csv_reader = csv.reader(file)
next(csv_reader)
for row in csv_reader:
question = row[0]
answer = row[1]
dataset.append((question, answer))
train_size = int(0.8 * len(dataset))
training_set = dataset[:train_size]
test_set = dataset[train_size:]
def normalized_compression_distance(x1, x2):
#C(x) and C(y) are the compressed sizes of strings x and y, respectively.
Cx1 = len(gzip.compress(x1.encode()))
Cx2 = len(gzip.compress(x2.encode()))
x1x2 = " ".join([x1, x2])
#C(xy) is the compressed size of the concatenated strings x and y.
Cx1x2 = len(gzip.compress(x1x2.encode()))
#min{C(x), C(y)} represents the smallest compressed size between x and y.
#max{C(x), C(y)} represents the largest compressed size between x and y.
ncd = (Cx1x2 - min(Cx1, Cx2)) / max(Cx1, Cx2)
return ncd
# Function to predict the class for a given text using KNN
def predict_class_knn(text, dataset, k=3):
distances = []
for (question, answer) in dataset:
distance = normalized_compression_distance(text, question)
distances.append((distance, answer))
distances.sort(key=lambda x: x[0])
top_k_class = [distances[i][1] for i in range(k)]
predicted_class = max(set(top_k_class), key=top_k_class.count)
return predicted_class
I tried random things since I didn’t know and couldn’t remember exactly what my conversations were about, but I couldn’t get a fully efficient result. However, I was surprised at one point because when I left a blank or entered meaningless letters or numbers, I received this response
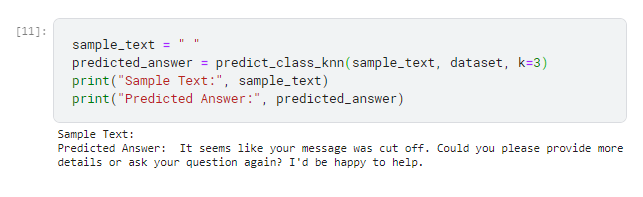
Afterward, I collected approximately 300 data points from a law website and decided to give it a try, and the result was surprising. I felt as if I was performing a sort of search, but the result was good. It gave a lot of wrong results in some places, but for now, it was satisfactory.
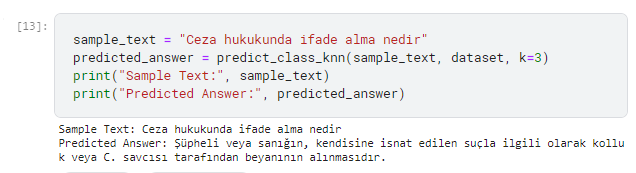
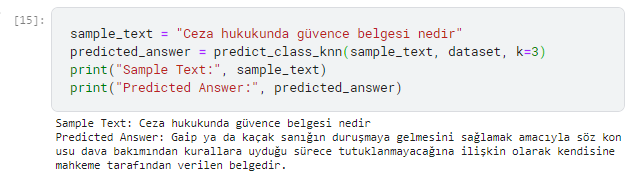

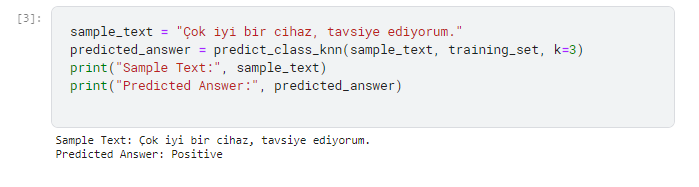
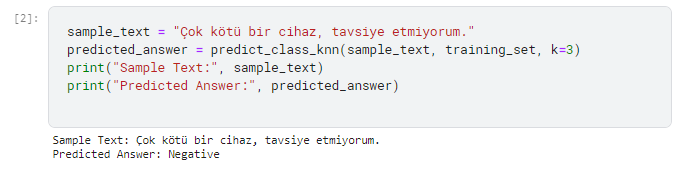
I also tested model on Sentiment Analysis with winvoker’s Turkish Sentiment Analysis Dataset and results are very good. It works quickly and effectively.
import gzip
import numpy as np
import datasets
dataset = datasets.load_dataset("winvoker/turkish-sentiment-analysis-dataset", split="train")
questions = dataset['text']
answers = dataset['label']
data_tuples = list(zip(questions, answers))
train_size = int(0.8 * len(data_tuples))
training_set = data_tuples[:train_size]
test_set = data_tuples[train_size:]
def normalized_compression_distance(x1, x2):
#C(x) and C(y) are the compressed sizes of strings x and y, respectively.
Cx1 = len(gzip.compress(x1.encode()))
Cx2 = len(gzip.compress(x2.encode()))
x1x2 = " ".join([x1, x2])
#C(xy) is the compressed size of the concatenated strings x and y.
Cx1x2 = len(gzip.compress(x1x2.encode()))
#min{C(x), C(y)} represents the smallest compressed size between x and y.
#max{C(x), C(y)} represents the largest compressed size between x and y.
ncd = (Cx1x2 - min(Cx1, Cx2)) / max(Cx1, Cx2)
return ncd
# Function to predict the class for a given text using KNN
def predict_class_knn(text, dataset, k=3):
distances = []
for (question, answer) in dataset:
distance = normalized_compression_distance(text, question)
distances.append((distance, answer))
distances.sort(key=lambda x: x[0])
top_k_class = [distances[i][1] for i in range(k)]
predicted_class = max(set(top_k_class), key=top_k_class.count)
return predicted_class

Article
“Low-Resource” Text Classification: A Parameter-Free Classification Method with Compressors (Jiang et al., Findings 2023)